DAG (Directed Acyclic Graph)
DAG는 순환을 가지지 않는 방향 그래프를 말한다.
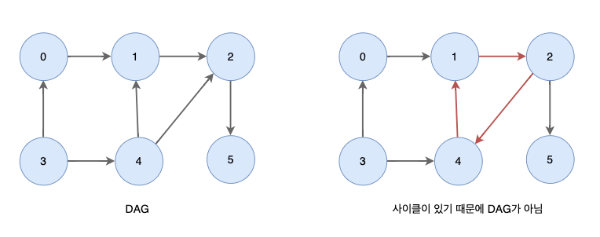
- 일반적으로 우선순위를 가진 일련의 작업들은 DAG 구조를 가진다.
- DAG에서 어떤 정점 \(v_i \in V, v_j \in V\) 에 대해서 \(v_i\) 에서 \(v_j\) 로의 경로가 존재하면, \(v_i\) 는 \(v_j\) 의 선행자이고 \(v_j\) 는 \(v_i\) 의 후행자이다.
- DAG에서 어떤 정점 \(v_i \in V, v_j \in V\) 에 대해서 \(v_i\) 에서 \(v_j\) 로의 간선이 존재하면, \(v_i\) 는 \(v_j\) 의 즉각 선행자이고 \(v_j\) 는 \(v_i\) 의 즉각 후행자이다.
위상정렬
DAG에서 그래프의 방향성을 거스르지 않고 정점들을 나열하는 것을 말한다.
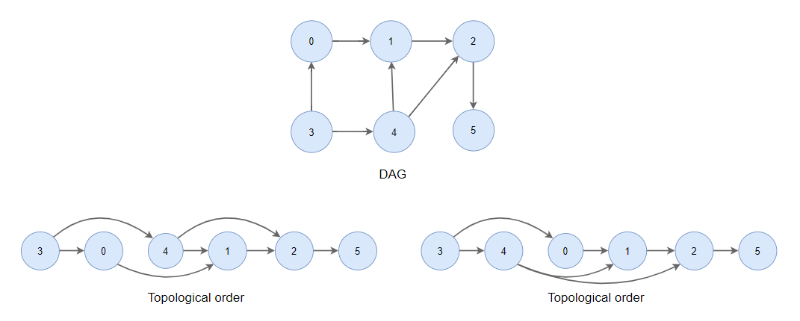
위상정렬은 각 정점을 우선순위에 따라 배치한 것이다.
일반적으로 위상정렬의 결과는 유일하지 않다.
구현
위상정렬을 구현하는 방법에는 in-degree를 이용한 BFS 방법과 DFS 방법이 있다.
- 각 정점의 in-degree를 저장할 배열을 만든다.
- in-degree가 0인 정점은 방문한 것으로 표시하고 큐에 해당 정점을 추가한다.
- 큐의 맨 앞에 있는 정점을 하나 빼낸다.
- 해당 정점에 인접한 정점들 중 방문하지 않은 정점의 in-degree를 하나 감소시킨다.
- in-degree가 0인 된 정점이 있다면 방문한 것으로 표시하고 큐에 해당 정점을 추가한다.
- 큐가 비어있을 때까지 3번~5번 작업을 반복한다.
- 처음 시작할 정점을 하나 고른다.
- 방문한 것으로 표시하고 간선을 따라 해당 정점에 인접한 정점들을 방문한다.
- 더 이상 방문할 곳이 없으면 리스트 앞에 현재 정점을 추가한다.
- 백트랙킹을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인한다.
- 방문 가능한 간선이 있다면 다시 해당 간선을 따라 다음 정점으로 이동한다.
- 모든 정점을 방문할 때까지 2번~5번 과정을 반복한다.
728x90
반응형
'알고리즘 > 그래프' 카테고리의 다른 글
| [CS] 최소 신장 트리와 구현 알고리즘 (JAVA) (0) | 2023.03.29 |
|---|---|
| [백준] 1717번 집합의 표현 (JAVA) (0) | 2023.03.16 |
| [CS] 서로소 집합 (JAVA) (0) | 2023.03.16 |
| [백준] 1516번 게임 개발 (JAVA) (0) | 2023.03.12 |
| [CS] 그래프 이론 (0) | 2023.03.11 |
DAG (Directed Acyclic Graph)
DAG는 순환을 가지지 않는 방향 그래프를 말한다.

- 일반적으로 우선순위를 가진 일련의 작업들은 DAG 구조를 가진다.
- DAG에서 어떤 정점
- DAG에서 어떤 정점
위상정렬
DAG에서 그래프의 방향성을 거스르지 않고 정점들을 나열하는 것을 말한다.

위상정렬은 각 정점을 우선순위에 따라 배치한 것이다.
일반적으로 위상정렬의 결과는 유일하지 않다.
구현
위상정렬을 구현하는 방법에는 in-degree를 이용한 BFS 방법과 DFS 방법이 있다.
- 각 정점의 in-degree를 저장할 배열을 만든다.
- in-degree가 0인 정점은 방문한 것으로 표시하고 큐에 해당 정점을 추가한다.
- 큐의 맨 앞에 있는 정점을 하나 빼낸다.
- 해당 정점에 인접한 정점들 중 방문하지 않은 정점의 in-degree를 하나 감소시킨다.
- in-degree가 0인 된 정점이 있다면 방문한 것으로 표시하고 큐에 해당 정점을 추가한다.
- 큐가 비어있을 때까지 3번~5번 작업을 반복한다.
- 처음 시작할 정점을 하나 고른다.
- 방문한 것으로 표시하고 간선을 따라 해당 정점에 인접한 정점들을 방문한다.
- 더 이상 방문할 곳이 없으면 리스트 앞에 현재 정점을 추가한다.
- 백트랙킹을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인한다.
- 방문 가능한 간선이 있다면 다시 해당 간선을 따라 다음 정점으로 이동한다.
- 모든 정점을 방문할 때까지 2번~5번 과정을 반복한다.
728x90
반응형
광고
광고
'알고리즘 > 그래프' 카테고리의 다른 글
| [CS] 최소 신장 트리와 구현 알고리즘 (JAVA) (0) | 2023.03.29 |
|---|---|
| [백준] 1717번 집합의 표현 (JAVA) (0) | 2023.03.16 |
| [CS] 서로소 집합 (JAVA) (0) | 2023.03.16 |
| [백준] 1516번 게임 개발 (JAVA) (0) | 2023.03.12 |
| [CS] 그래프 이론 (0) | 2023.03.11 |

