[CS] 최소 신장 트리와 구현 알고리즘 (JAVA)

트리

무향 그래프이면서, 순환이 없는 연결 그래프

트리의 어떤 두 정점에 대해서 단순 경로가 하나 존재한다.

 

신장 트리

무향 연결 그래프의 부분 그래프이고, 해당 그래프의 모든 정점을 포함하는 트리

다음은 무향 연결 그래프에 대한 4가지 신장 트리이다. (E = V - 1)

출처 : https://limecoding.tistory.com/123

 

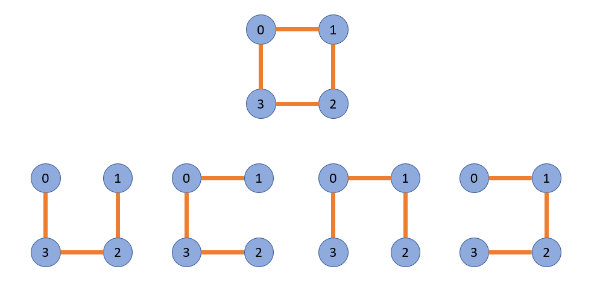
깊이 우선 신장 트리와 너비 우선 신장 트리

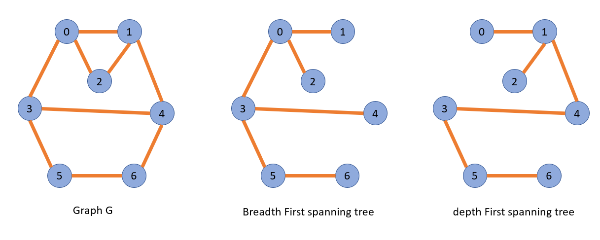
깊이 우선 신장 트리는 무향 연결 그래프에서 DFS으로 탐색하면서 생성된 신장 트리이다.
너비 우선 신장 트리는 무향 연결 그래프에서 BFS으로 탐색하면서 생성된 신장 트리이다.

출처 : https://limecoding.tistory.com/123

 

최소 신장 트리 (Minimum Spanning Tree / MST)

무향 연결 가중 그래프에서 간선의 가중치의 합이 최소인 신장 트리

출처 : https://velog.io/@suk13574/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%B5%9C%EC%86%8C-%EC%8B%A0%EC%9E%A5-%ED%8A%B8%EB%A6%AC

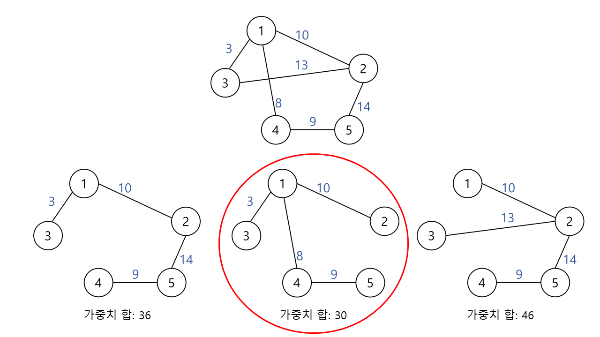
그래프에서 최소 신장 트리를 만드는 알고리즘으로는, 크루스칼 알고리즘과 프림 알고리즘이 있다.

 

크루스칼 알고리즘

간선을 중심으로 그리디 알고리즘을 통해 최소 신장 트리를 구하는 알고리즘

• 우선순위 큐를 이용하여 구현 (선택적)
• 시간복잡도 : \(O(ElogV)\)
• 동작 원리

1. 간선들을 오름차순으로 정렬한다.
2. 선택되지 않은 간선들 중 가중치가 가장 작은 간선을 선택한다.
3. 해당 간선을 선택했을 때, 사이클이 생기지 않은 경우에만 선택한다. (Union-Find 연산 이용)
4. 총 (V - 1) 개의 간선이 선택될 때까지 반복한다.

• 구현

int find(int element) {
    if (computers[element] == element)
        return element;
    else {
        return graph[element] = find(graph[element]);
    }
}

void union(int element1, int element2) {
    // element1과 element2의 대표 노드 확인
    int root1 = find(element1);
    int root2 = find(element2);

    // element1과 element2의 대표 노드가 다를 경우
    if (root1 != root2)
       graph[root1] = root2;
}
    
// 크루스칼 알고리즘
void kruskal() {
    int minCost = 0;
    
    while (!pq.isEmpty()) {
    	Edge edge = pq.poll();
        
        if (find(edge.current) != find(edge.dest)) {
            union(edge.current, edge.dest);
            minCost += edge.cost;
        }
    }
    
    System.out.println(minCost);
}

 

프림 알고리즘

간선을 정렬하지 않고 하나의 정점에서 시작하여 트리를 확장해 나가는 알고리즘

• 우선순위 큐를 이용하여 구현 (필수적)
• 시간복잡도 : \(O((E+V)logV)\)
• 동작 원리

1. 그래프에서 시작 정점을 선택한다.
2. 선택한 정점에 부속된 모든 간선 중 가중치가 가장 작은 간선을 선택해 연결한다.
3. 이전에 선택한 정점과 새로 확장된 정점에 부속된 모든 간선 중 가중치가 가장 작은 간선을 삽입한다.
4. 총 (V - 1) 개의 간선이 선택될 때까지 반복한다.

• 구현

// 간선의 정보 저장할 클래스
class Edge implements Comparable<Edge> {
    int dest; 	// 간선 도착 정점
    int cost; 	// 간선 가중치
	
    Edge(int dest, int cost){
	    this.dest = dest;
	    this.cost = cost;
    }
	
    // 간선 오름차순으로 정렬
    @Override
    public int compareTo(Edge edge) {
        return this.cost - edge.cost;
    }
}

// 프림 알고리즘
void prim(int start, int N) {
    boolean[] visited = new boolean[N + 1];
	
    PriorityQueue<Edge> pq = new PriorityQueue<>();
    pq.offer(new Edge(start, 0));
		
    int minCost = 0;
    
    while (!pq.isEmpty()) {
        Edge edge = pq.poll();
        int dest = edge.dest;
        int cost = edge.cost;
		
        // 방문 했다면 건너뜀
        if (visited[dest]) 
            continue;
        
        visited[dest] = true;
        minCost += cost;
		
        // 해당 정점에 연결되어 있는 모든 간선 탐색
        for (Edge e : graph.get(dest)) {
            if (!visited[e.dest]) 
                pq.add(e);
        }
    }
   
    System.out.println(minCost);
}